
机器学习算法-相关性分析
- 机器学习步骤:提出问题-理解数据-数据清洗-构建模型-评估
- 特征与标签的定义
特征:数据属性,例如音乐的节奏,强度,听歌时长
标签:数据预测结果,例如对某个歌曲的喜欢和不喜欢
- python机器学习包-sklearn
- 简单线性回归
- 什么是相关性分析:
虽然变量间有着十分密切的关系,但是不能由一个或多各变量值精确地求出另一个变量的值,称为相关关系,存在相关关系的变量称为相关变量
- 导入数据
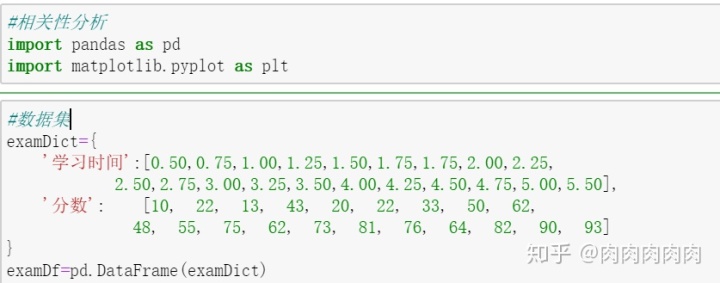
- 散点图绘制
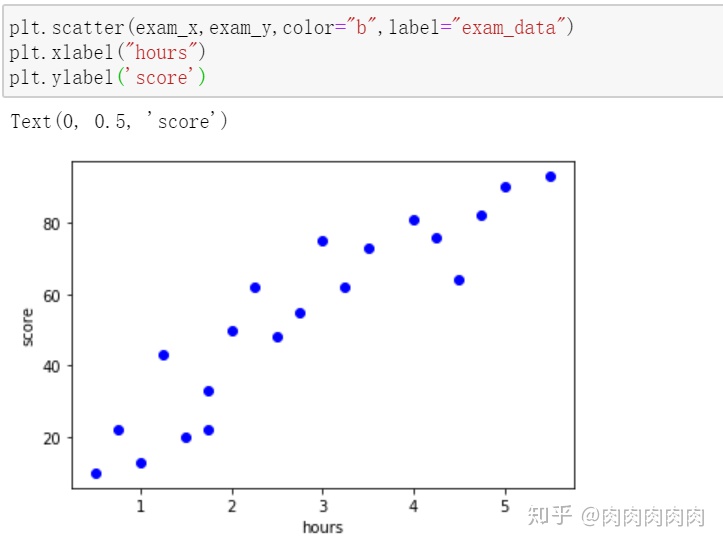
从散点图可以看出学习时间长短似乎和分数有着联系,学习时间越长分数增长的可能性也越大
- 3种线性相关性
1)正线性相关:直线朝上
2)负线性相关: 直线朝下
3)不是线性相关:随机分布
- 描述线性相关的统计量(两个变量的相关性方向,相关性大小)
- 协方差=E[(x-ux)(y-uy)]
协方差>0:两个变量同方向变化
协方差<0:两个变量反方向变化
协方差缺点:容易被变量的变化幅度大小影响,并不能反映相关性大小
2.相关系数=协方差/x的标准差*y的标准差
相关系数又名皮尔森积矩相关系数
相关系数是标准化后的协方差,[-1,1],相关系数大于零,表示两个变量正线性相关;相关系数小于零,表示两个变量负线性相关。相关系数等于零,表示两个变量之间不存在线性相关
相关系数大小:表示两个变量每单位的相关性程度
[0,0.3]:弱相关,[0.3,0.6]:中等程度相关,[0.6,1]:强相关
- 相关系数函数
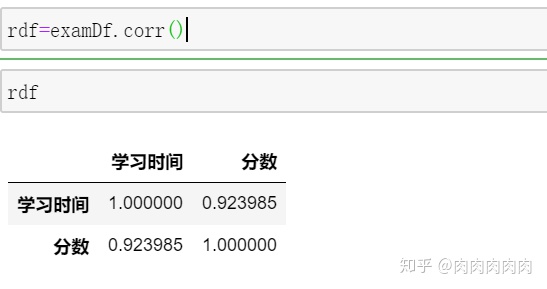
- 提取特征和标签

- 建立训练数据和测试数据
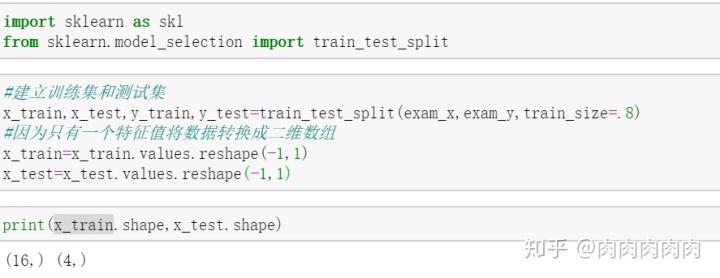
- 训练模型
- 报错信息
reshape行的参数是-1表示什么呢?例如reshape(-1,列数)如果行的参数是-1,就会根据所给的列数,自动按照原始数组的大小形成一个新的数组,例如reshape(-1,1)就是改变成1列的数组,这个数组的长度是根据原始数组的大小来自动形成的。原始数组总共是2行*3列=6个数,那么这里就会形成6行*1列的数组
reshape列的参数是-1表示什么呢?例如reshape(行数,-1)如果列的参数是-1,就会根据所给的行数,自动按照原始数组的大小形成一个新的数组,例如reshape(1,-1)就是改变成1行的数组,这个数组的列数是根据原始数组的大小来自动形成的。原始数组总共是2行*3列=6个数,那么这里就会形成1行*6列的数组
- 截距和回归系数

- 模型精确度评估
1)决定系数R平方
y误差平方和=(y实际值-y预测值)2求和
数据点的多少会影响误差平方和的大小
y总波动=(y实际值-y平均值)2求和
有多少百分比的y波动没有被回归线描述:误差平方和/总波动
有多少百分比的y波动被回归线描述:1-误差平方和/总波动=决定系数R平方
R平方越高,回归模型越精确
2)用python求r平方
- 相关关系和因果关系
相关关系:例如花粉量多和防晒霜销量多,只是相关关系
因果关系:花粉量说明天气好,人们会进行户外运动,因而防晒霜销量激增,户外运动和防晒霜销量增加才具有因果关系