弹性网络_正则化(3)：弹性网络回归

引言：在前面一小节中我们 指出，在含有多个参数的模型中，如何做出对模型的优化。岭回归更好？还是lasso回归更优？参考：正则化(2)：与岭回归相似的 Lasso 回归。 在这种情况下，还要一种折中的办法，就是选择弹性网络回归(Elastic Net Regression)。

1. lasso回归与岭回归的异同

• 如下，如果已知模型中的很多变量为无关变量，如astrological offset和airspeed scalar等，我们倾向于选择lasso回归，从而使得拟合模型更加简洁和便于解读。

Size = y-intercept + slope x Weight + diet differece x Hight Fat Diet +

                   + astrological offset x Sign + airspeed scalar x Airspeed of Swallow

• 如下，如果模型中有非常多的变量，我们无法知道其是否是无关变量，如基于10000个基因的表达预测小鼠体积。在这种情况下，我们应该选择lasso回归，还是岭回归呢？

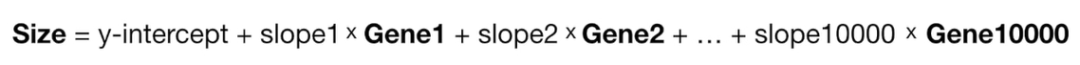
• 答案是弹性网络回归(Elastic Net Regression)。听名字非常炫酷，有弹性的回归，意味着它非常灵活能适应多用场景。简单来说，弹性网络回归是lasso回归和岭回归的结合版本。

2. 弹性网络回归是lasso回归和岭回归的结合版

公式解读：弹性网络回归包含lasso回归和岭回归非惩罚项，两种惩罚项的λ系数不同(lasso回归λ1，岭回归λ2)。基于使用多个不同λ1和λ2的交叉验证，以寻找最佳λ1和λ2的取值。

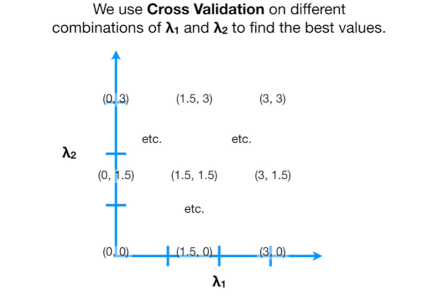
• 当λ1 = 0，λ2 = 0时，弹性网络回归与最初的最小二乘法线性回归拟合的模型一致。

• 当λ1 = 0，λ2 ＞ 0时，弹性网络回归与lasso回归拟合的模型一致。

• 当λ1＞0，λ2 = 0时，弹性网络回归与岭回归拟合的模型一致。

• 当λ1＞0，λ2＞0时，弹性网络回归为岭回归和lasso回归的结合版本。

3. 弹性网络回归具有lasso回归与岭回归的优点

弹性网络回归善于解决含有相关性参数的模型：lasso回归筛选出相关的参数，并缩减其他无关参数；同时岭回归缩减所有相关性的参数。

通过二者的结合，弹性网络回归可以筛选和缩减具有相关性的参数，将他们保留在模型中或者从模型中移除。在处理具有相关性的参数时，弹性网络回归能够表现出良好的性能。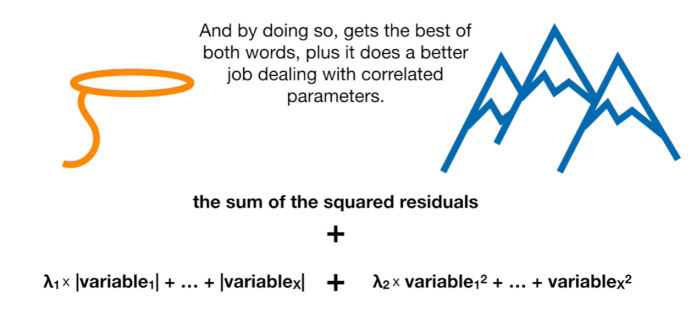

参考视频：

1.岭回归。

https://www.youtube.com/watch?v=Q81RR3yKn30&list=PLblh5JKOoLUICTaGLRoHQDuF_7q2GfuJF&index=19

2.lasso回归。

https://www.youtube.com/watch?v=NGf0voTMlcs&list=PLblh5JKOoLUICTaGLRoHQDuF_7q2GfuJF&index=20

3.弹性网络回归。

https://www.youtube.com/watch?v=1dKRdX9bfIo&list=PLblh5JKOoLUICTaGLRoHQDuF_7q2GfuJF&index=22

编辑：吕琼

校审：罗鹏