###RSA gmpy2函数实现.
一.pow:
1 .分奇偶性去用递归函数迭代计算:
def mypow(x:float,y:int) ->float:
if y == 0:
return 1
if y%2 == 0:
return mypow(x*x,y//2)
if y%2 == 1:
return x*mypow(x,y-1)
2 .快速幂方法:
计算a的b次方,需要考虑:
1、b==0 的话,返回1
2、b<0的情况,设置一个flag,用于返回数据的时候进行判断
3、b>0的情况:
def Power(self, base, exponent):
# write code here
flag=1
re=1
tmp=base
if exponent==0: #等于0的情况
return 1
if exponent<0: #小于0的时候,设置一个flag,用于返回的时候做判断
flag=0
exponent=abs(exponent)
while exponent>0: #大于0的情况
if exponent&1==1:
re=re*tmp #如果是奇数,奇数减一就是偶数
exponent>>=1 #右移动一位就是除以2
tmp=tmp*tmp #2^6=(2*2)^3
return re if flag else 1/re
二.powmod
即在pow的属性上再加上一个输入值 为mod 的东西,再在输出时 原来pow得出的值取mod
三.long_to_bytes
1.long:长整数类型,无限大小
2.bytes:是指一堆字节的集合,十六进制表现形式,两个十六进制数构成一个 byte ,以 b 开头的字符串都是 bytes 类型。
def long_to_bytes(a:int) -> str:
m=hex(a)
q=m[2:]
t=bytes.fromhex(q)
return t
四.产生大素数
欧拉筛法代码:
def get_prime(n):
isPrime= [False for i in range(2, n+3)]
prime = []
for i in range(2, n):
if isPrime[i] is False:
prime.append(i)
for j in prime:
if i * j > n:
break
isPrime[i * j] = True
if i % j == 0:
break
return prime
print(get_prime(120))
```
五.通过Miller-Rabin素数检测方法实现大素数的随机产生
1.两个基础定理
a.费马小定理:当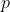 为质数,有
为质数,有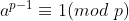 ,不过反过来不一定成立,也就是说,如果
,不过反过来不一定成立,也就是说,如果 ,
,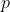 互质,且
互质,且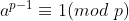 ,不能推出
,不能推出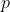 是质数,比如
是质数,比如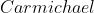 数(这个就自行百度吧)
数(这个就自行百度吧)
b.二次探测:如果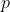 是一个素数,
是一个素数,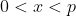 , 则方程
, 则方程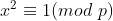 的解为
的解为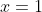 或
或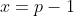
2.两个基本定理的证明

3.算法流程:
(1)对于偶数和 0,1,2 可以直接判断。
(2)设要测试的数为,我们取一个较小的质数
,设
,满足
(其中
是奇数)。
(3)我们先算出,然后不断地平方并且进行二次探测(进行
次)。
(4)最后我们根据费马小定律,如果最后,则说明
为合数。
(5)多次取不同的进行
素数测试,这样可以使正确性更高
4.备注:
(1)我们可以多选择几个,如果全部通过,那么
大概率是质数。
(2)素数测试中,“大概率”意味着概率非常大,基本上可以放心使用。
(3)当取遍小等于 30 的所有素数时,可以证明
范围内的数不会出错。
(4)代码中我用的类型,不过实际上
素数测试可以承受更大的范围。
(5)另外,如果是求一个类型的平方,可能会爆掉,因此有时我们要用“快速积”,不能直接乘。
5.代码块:
#Miller_Rabin素数检测 方法.
def Miller_Rabin(n):
if n == 2 or n == 3:
return True
if n & 1 == 0:
return False
s, d = 0, n - 1
while d % 2 == 0:
s += 1
d //= 2
for i in pip._vendor.msgpack.fallback.xrange(80): # 进行80轮检验
# xrange() 函数用法与 range 完全相同,所不同的是生成的不是一个数组,而是一个生成器。
a = randrange(2, n - 1) # 按递增的方式产生随机数
# randrange() 方法返回指定递增基数集合中的一个随机数,基数默认值为1。
k = pow(a, d, n) # k = a^d mod n
if k == 1 or k == n - 1:
continue
# 对Miller序列测试
for r in pip._vendor.msgpack.fallback.xrange(s):
k = pow(k, 2, n) # k = a ^[(2^r)*d] mod n
if k == n - 1:
break
else:
return False
return True
# 产生大素数
def getPrime(n):
if n <= 2:
return False
while True:
t = '1'
for i in range(n - 2):
t += str(randint(0, 1))
t += '1'
t = int(t, 2)
if Miller_Rabin(t):
return t
六.裴蜀定理
1.内容:若a,b是整数,且gcd(a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立。
2.重要推论:a,b互质的充分必要条件是存在整数x,y使ax+by=1
七.invert 函数实现:
1.已知
d ∗ e ≡ 1 ( m o d φ ( n ) ) d*e≡1(mod φ(n))d∗e≡1(modφ(n))
( e , φ ( n ) ) = 1 (e,φ(n))=1(e,φ(n))=1
a = e , y = φ ( n ) a=e,y=φ(n)a=e,y=φ(n)
e x + φ ( n ) y = 1 ex+φ(n)y=1ex+φ(n)y=1
e x ≡ 1 ( m o d ϕ ( n ) ) ex \equiv1(mod \phi(n))ex≡1(modϕ(n))
只需解出x的整数解即可
2.所以可以通过推导得出
gcd, d, y = exgcd(e, phi)
temp = phi // gcd
# 解出ed=1(mod phi)的最小正整数解,
d = (d % phi + phi) % phi
即可以得出d的最小整数解
版权声明:本文为DeeBaTO原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。