MATLAB神经网络编程（四）——线性神经网络的实现与局限

**MATLAB神经网络编程》 化学工业出版社 读书笔记
第四章 前向型神经网络 4.2 线性神经网络**

本文是《MATLAB神经网络编程》书籍的阅读笔记，其中涉及的源码、公式、原理都来自此书，若有不理解之处请参阅原书。

一，线性神经网络的实现。

线性神经网络在模式识别、信号滤波和预测、函数逼近等方面有广泛的用途，下面用实例来说明线性神经网络的MATLAB仿真程序设计。

1，线性神经网络在模式分类中的应用。
【例4-16】一单层线性神经网络模拟与函数。

根据与函数的性质，与函数是一个简单的线性划分问题，用一个线性神经元构成的网络就可以实现。基本结构：

• 网络有一个输入向量，包括2个元素，输入元素的取值范围[0 1]

• 输出有一个元素，为二值变量0或1
  设计的线性神经网络的结构示意图如下：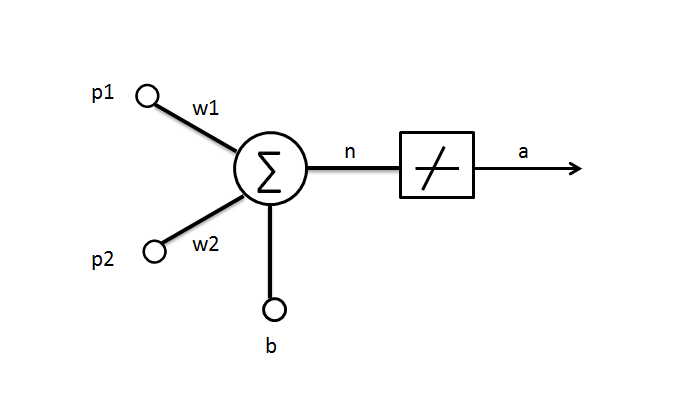

  

源代码：

clear all;
%设计线性神经网络
p=[0 0;0 1;1 0;1 1]';   %输入向量
t=[0 0 0 1];       %输出向量
net=newlind(p,t)    %设计线性神经网络
w=net.iw{1}
b=net.b{1};
%线性神经网络的仿真
a=sim(net,p)     %输出仿真结果
y=a>0.5      %将模拟仿真结果转换为数字量

输出为：

w =

    0.5000    0.5000


b =

   -0.2500


a =

   -0.2500    0.2500    0.2500    0.7500


y =

     0     0     0     1

2，线性神经网络在噪声对消中的应用。

【例4-17】（以自适应线性神经网络实现噪声对消）对于一个最优的滤波器希望通过滤波将信号中的噪声去掉，这对于一般的滤波器来说很难完全做到。利用自适应线性神经网络实现噪声对消的原理：

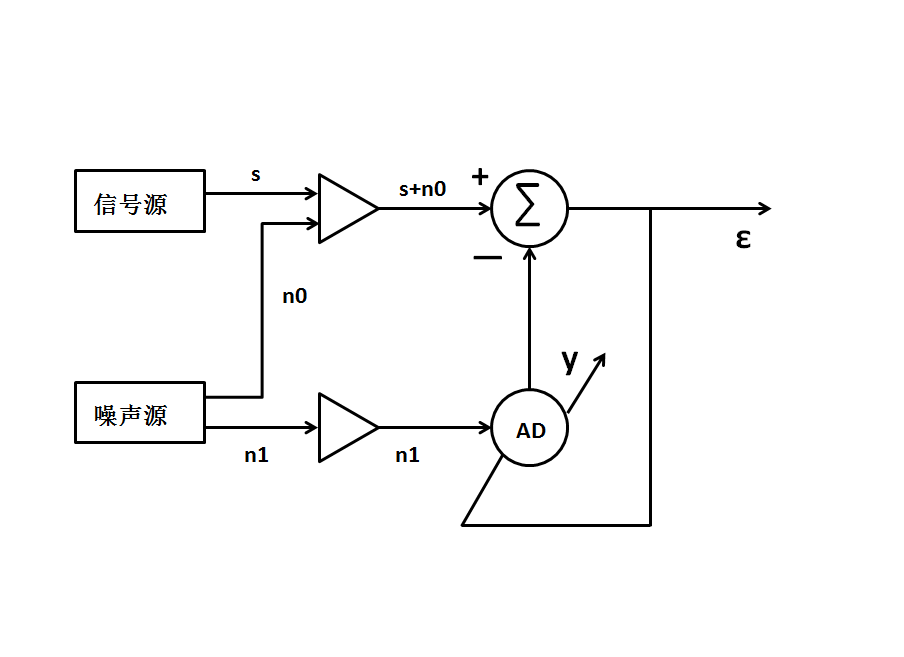
上图中s为原始输入信号，假设为平稳的零均值随机信号；n0为与s不相关的随机噪声；
n1为与n0相关的信号；系统输出为ε；s+n0为ADALINE神经元的预期输出；y为ADALINE神经元的输出。则：

ε=s+n0-y

可知当y->n0时ε=s

关于噪声对消的原理可以参考文档：http://www.doc88.com/p-5718140232621.html
http://www.docin.com/p-376010503.html

源代码：

clear all;
%定义输入向量和目标向量
time=0.01:0.01:10;             %时间变量
noise=(rand(1,1000)-0.5)*4;    %随机噪声
input=sin(time);               %输入信号
p=noise;                       %将噪声作为ADALINE的输入向量
t=input+noise;                 %将噪声+信号作为目标向量
                               %创建线性神经网络
net=newlin([-1 1],1,0,0.0005);
%线性神经网络的训练
net.adaptParam.passes=70;
[net,y,output]=adapt(net,p,t);    %output为网络调整过程的误差
%绘制信号
hold on;
subplot(3,1,1);
plot(time,input,'r');
title('信号波形sin(t)');

subplot(3,1,2);
plot(time,t,'m');                  %绘制叠加信号
xlabel('t');
title('随机噪声波形sin(t)+noise(t)');
%绘制输出信号的波形
subplot(3,1,3);
plot(time,output,'b');
xlabel('t');
title('输出信号波形y(t)');

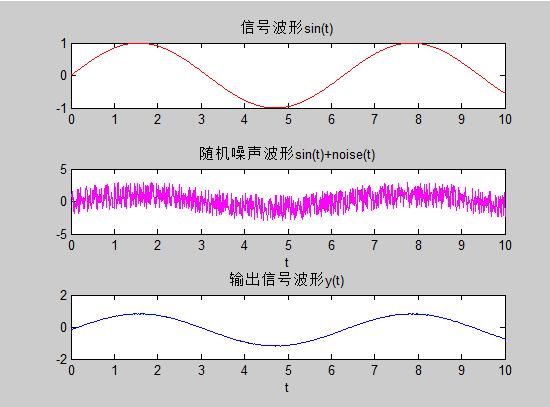
输出结果：

3，线性神经网络在信号预测中的应用。

源码：

clear all;
% 定义输入向量和目标向量
time=0.5:0.5:20;         %时间变量
y=(rand(1,40)-0.5)*4;    %定义随机输入信号
p=con2seq(y);            %将随机输入向量转换为串行向量
delays=[1 2];            %定义ADALINE神经元输入延迟量
t=p;                     %定义ADALINE神经元的数目向量
% 创建线性神经网络
net=newlin(minmax(y),1,delays,0.0005);
% 线性神经网络的自适应调整(训练)
net.adaptParam.passes=70;
[net,a,output]=adapt(net,p,t);  %输出信号output为网络调整过程中的误差
% 绘制随机输入信号\输出信号的波形
hold on;
subplot(3,1,1);plot(time,y,'r*-'); %输出信号output为网络调整过程中的误差
xlabel('t','position',[20.5,-1.8]);
ylabel('随机输入信号s(t)');
axis([0 20 -2 2]);
subplot(3,1,2);
output=seq2con(output);
plot(time,output{1},'ko-');  %绘制预测输出信号的波形
xlabel('t','position',[20.5,-1.8]);
ylabel('预测输出信号y(t)');
axis([0 20 -2 2]);
subplot(3,1,3);
e=output{1}-y;
plot(time,e,'k-');   %绘制误差曲线
xlabel('t','position',[20.5,-1.8]);
ylabel('误差曲线e(t)');
axis([0 20 -2 2]);
hold off;

输出：

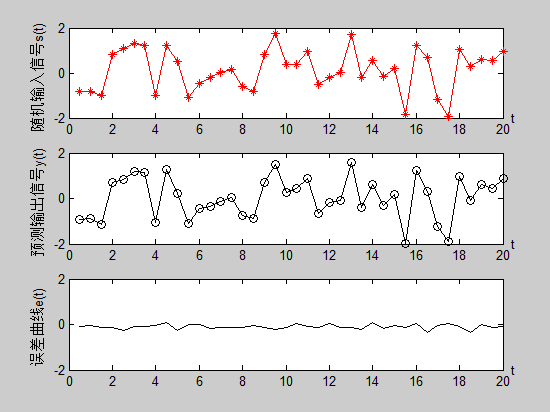
从图上可以看出，输出信号波形与输入信号波形基本一致，误差较小，输出波形较好的预测了输入波形。

值得一提的还是学习速率与训练步长的选择。如果学习速率过大，即学习的过程将不稳定，且误差会更大；反正如果学习速率过小，学习的过程将变慢，需要的训练步长将加大。
就线性神经网络本身来说，其余感知器一样，只能解决线性可分的模式分类，但LMS算法比感知器的δ学习算法更有效，因为它使均方误差最小，可以使各分类模式远离判决边界，从而使网络具有更好 的抗噪性。另一方面，ADALINE网络至今仍然广泛应用于各种实际系统中，特别是在自适应滤波方面，用途更加广泛。

二，线性神经网络的局限性。

线性神经网络只能反映输入和输出样本矢量间的线性映射关系，与感知器一样，其也只能解决线性可分问题。 由于线性神经网络的误差曲面为一个多维抛物面，所以在学习速率足够小的情况下对于基于最下二乘梯度下降原理进行训练的线性神经网络总可以找到一个解。但是，线性神经网络的训练不一定总能达到零误差。如果线性神经网络的自由度（即线性神经网络所有权值和阈值的个数总和）小于训练样本集中”输入-目标“矢量的对数，而且各样本矢量线性无关，则网络训练不可能达到零误差，只能达到一个使网络误差最小的解；反之，如果网络自由度大于样本集的个数，即会得到无穷多个使网络训练误差为零的解。

上述关于自由度判断可以理解为：S*R+S>=Q；此时可以用线性神经网络来解决。
但是当输入样本线性相关或者没有阈值的时候，这个公式不使用。

1，学习速率过大。

学习速率的选取是影响收敛速度以及训练结果的重要因素。学习速率足够小，根据W-H学习规则总能训练网络满足精度要求；学习速率过大，可能会导致训练过程不稳定。MATLAB工具箱提供了函数maxlinlr来求正确的学习速率。
【例4-19】

P=[+1.0 -1.2];
T=[+0.5 +1.0];
w_range=-2:0.4:2;
b_range=-2:0.4:2;
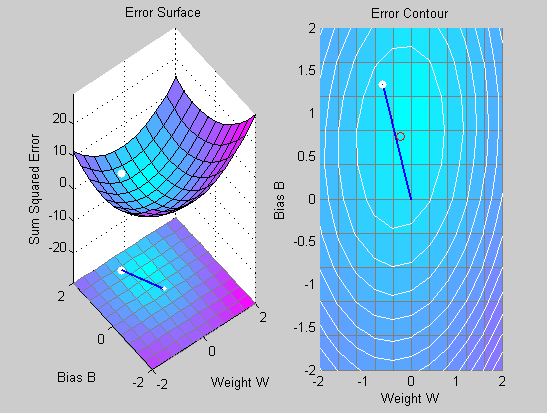
ES=errsurf(P,T,w_range,b_range,'purelin');
plotes(w_range,b_range,ES);
maxlr=maxlinlr(P,'bias');
net=newlin([-2 2],1,[0],maxlr*2.25);
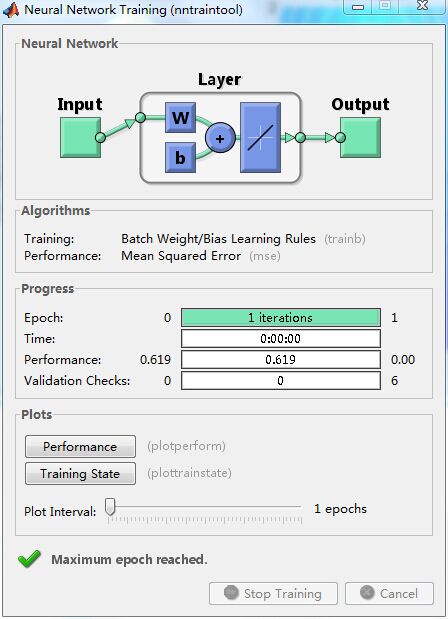
net.trainParam.epochs=20;
net.trainParam.epochs=1;
net.trainParam.show=NaN;
h=plotep(net.IW{1},net.b{1},mse(T-sim(net,P)));
[net,tr]=train(net,P,T);
r=tr;
epoch=1;
while epoch<20
    epoch=epoch+1;
    [net,tr]=train(net,P,T);
    if length(tr.epoch)>1
        h=plotep(net.IW{1,1},net.b{1},tr.perf(2),h);
        r.epoch=[r.epoch epoch];
        r.perf=[r.perf tr.perf(2)];
        v.vperf=[r.vperf NaN];
        r.tperf=[r.tperf NaN];
    else
        break
    end
end
tr=r;
solvednet=newlind(P,T);
hold on;
plot(solvednet.IW{1},solvednet.b{1},'ro')
hold off;
subplot(1,2,2);
plotperf(tr,net.trainParam.goal);
p=-1.2;
a=sim(net,p)

输出：

输出为：

a =

    2.0913

期望输出t=0.1，而网络输出a=1.0913。可见当学习速率选取过大时，误差越来越大，网络训练无法达到精度。

2，线性相关向量。

在应用线性神经网络之前首先要判断该问题是否能用线性神经网络来解决。通常，线性网络的自由度（权值与阈值总和S*R+S）至少要等于约束的数目（输入/输出样本数Q），这样才能应用。但是当输入样本相关或者没有阈值的时候，这种要求就可能不成立。如果线性相关的输入向量与期望输出向量之间并不匹配，那么此问题就是一个非线性问题，而且这个问题得不到零误差解。

【例4-20】假设输入向量和期望向量如下：
P=[1.0 2.0 3;4 5 6]
T=[0.5 1 -1]
可知输入向量具有相关性，而期望输出向量并不具备这种相关性，即输入/输出不匹配。那么即使有正确的学习速率等参数，结果也不如人意：

P=[1.0 2.0 3.0;4.0 5.0 6.0];
T=[0.5 1.0 -1.0];
maxlr=maxlinlr(P,'bias');
net=newlin([0 10;0 10],1,[0],maxlr);
net.trainParam.show=50;
net.trainParam.epochs=500;
net.trainParam.goal=0.001;
[net,tr]=train(net,P,T);
p=[1.0;4];
a=sim(net,p)

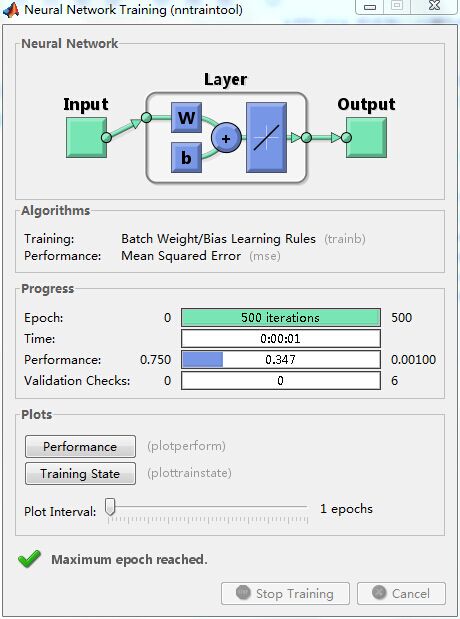
输出：

a =
0.8971

达到最大训练次数之后，仿真停止，但是训练精度没有的达到。可以得知：线性网络不能适应输入向量之间具有线性相关性的非线性问题。