python 机器学习 预处理和主成分分析(PCA)

预处理和主成分分析(PCA)
目的：

1. 学会对数据进行预处理与缩放
2. 学会使用PCA进行降维
3. 初步了解相关参数
   要求：
   基于乳腺癌数据集完成以下任务：
   1、乳腺癌数据的特征值有多少？
   2、写出数据变换的一般步骤
   3、将数据进行StandardScale，MinMaxScaler和RobustScaer转换
   4、在第三步骤的基础上，选择两个主成分，三个主成分利用LinearSVC分别器，求不同情况下的精度（测试集的精度）。

因为考虑到每次切片的random_state都不同，为了使测试精度更有说服力，每次给出的精度都经过n次切片训练，n是自己设定的。

1、 乳腺癌数据的特征值

#获取数据集
cancer = load_breast_cancer()
print(cancer.data.shape)

可以看到输出结果：

所以乳腺癌数据有30个特征

2、 数据变换的一般步骤：
1） 建立模型（以StandardScale为例） st_Scaler = StandardScaler()
2） 训练模型 st_Scaler.fit(cancer.data)
3） 数据转换 cancer_stScaler = st_Scaler.transform(cancer.data)

4、 在第三步骤的基础上，选择两个主成分，三个主成分利用LinearSVC分别器，求不同情况下的精度（测试集的精度）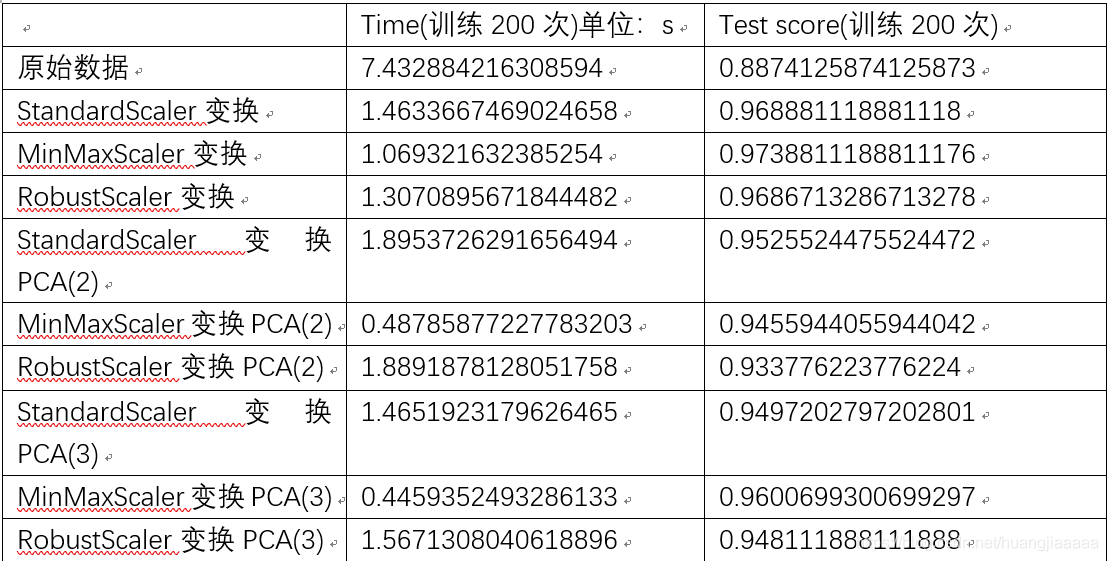

基于上表，我们可以看出数据经过变换处理后，训练速度有明显的提升，精度也提升了，所以可以看出对数据的处理是非常必要的，不仅能提升时间性能，还能提升测试的精度。PCA降维是为了降低分析的难度，当一个数据集的特征非常非常多的时候，我们通常要很费时间的去训练，但是通过上表我们可以看出，这个数据集原本是30维，降到2维以后，测试精度也并没下降，反而有所上升，所以我们认为，当数据集有大量的特征，进行PCA降维是有必要的。
完整代码：

# -*- coding: utf-8 -*-
"""
Created on Fri Nov 15 20:20:17 2019

@author: asus
"""

"""
预处理和主成分分析(PCA)
目的：
1.	学会对数据进行预处理与缩放
2.	学会使用PCA进行降维
3.	初步了解相关参数
要求：
基于乳腺癌数据集完成以下任务：
1、乳腺癌数据的特征值有多少？
2、写出数据变换的一般步骤
3、将数据进行StandardScale，MixMaxScaler和RobustScaer转换
4、在第三步骤的基础上，选择两个主成分，三个主成分利用LinearSVC分别器，求不同情况下的精度（测试集的精度）。
#注意
数据集使用
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
"""

import mglearn
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing  import StandardScaler
from sklearn.decomposition import PCA
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import RobustScaler
from sklearn.preprocessing import Normalizer
from sklearn.svm import LinearSVC
import time
import warnings
warnings.filterwarnings("ignore")#消除警告




def Linear_svc_mean_Score(data_set,target_set,num):
    """
    来一组数据，训练num次，返回linear_svc的训练集与测试集的平均得分
    入口参数为数据集，目标数据集，训练次数
    """
    train_scores = []
    test_scores = []
    start = time.time()
    for i in range(num):
        X_train,X_test,y_train,y_test = train_test_split(data_set,target_set,stratify = target_set)
        linear_svc.fit(X_train,y_train)
        train_score = linear_svc.score(X_train, y_train)
        test_score = linear_svc.score(X_test, y_test)
        train_scores.append(train_score)
        test_scores.append(test_score)
    
    print("Time used :",time.time() - start)
    train_mean_scores = sum(train_scores) / len(train_scores)
    test_mean_scores = sum(test_scores) / len(test_scores)
    return (train_mean_scores,test_mean_scores)

#获取数据集
cancer = load_breast_cancer()
print(cancer.data.shape)
print(cancer.target.shape)

#对原始数据切片
X_train,X_test,y_train,y_test = train_test_split(cancer.data,cancer.target,stratify = cancer.target,random_state = 0)

#建立模型
linear_svc = LinearSVC()
#训练模型
linear_svc.fit(X_train,y_train)
#对原始数据训练队的模型进行评估
#print("The train scores of Raw data :",linear_svc.score(X_train,y_train))
#print("The test scores of Raw data :",linear_svc.score(X_test,y_test))
#print("Raw data : ",X_train.shape,X_train[0])

#训练60次
num = 200

train_mean_scores,test_mean_scores = Linear_svc_mean_Score(cancer.data,cancer.target,num)
#print("The train scores of Raw data :",train_mean_scores)
print("The test scores of Raw data :",test_mean_scores)


#将数据进行StandardScale变换
st_Scaler = StandardScaler()
st_Scaler.fit(cancer.data)
cancer_stScaler = st_Scaler.transform(cancer.data)
train_mean_scores,test_mean_scores = Linear_svc_mean_Score(cancer_stScaler,cancer.target,num)
#print("The train scores of StandardScaler transformed data :",train_mean_scores)
print("The test scores of StandardScaler transformed data :",test_mean_scores)

#在StandardScale基础上，选择两个主成分
pca = PCA(n_components = 3)
pca.fit(cancer_stScaler)
X_pca = pca.transform(cancer_stScaler)
X_train,X_test,y_train,y_test = train_test_split(X_pca,cancer.target,stratify=cancer.target,random_state=60)
#查看PCA降维后的数据类型
print("PCA(2) data : " ,X_train.shape,X_train[0])
train_mean_scores,test_mean_scores = Linear_svc_mean_Score(X_pca,cancer.target,num)
#print("The train scores of StandardScaler transformed(PCA(2)) data :",train_mean_scores)
print("The test scores of StandardScaler transformed(PCA(2)) data :",test_mean_scores)

#将数据进行MixMaxScaler变换
M_scaler = MinMaxScaler()
M_scaler.fit(cancer.data)
cancer_M_Scaler = M_scaler.transform(cancer.data)
train_mean_scores,test_mean_scores = Linear_svc_mean_Score(cancer_M_Scaler,cancer.target,num)
#print("The train scores of MinMaxScaler transformed data :",train_mean_scores)
print("The test scores of MinMaxScaler transformed data :",test_mean_scores)

#在MixMaxScaler基础上，选择两个主成分
pca = PCA(n_components = 3)
pca.fit(cancer_M_Scaler)
X_pca = pca.transform(cancer_M_Scaler)
X_train,X_test,y_train,y_test = train_test_split(X_pca,cancer.target,stratify=cancer.target,random_state=60)
#查看PCA降维后的数据类型
print("PCA(2) data : " ,X_train.shape,X_train[0])
train_mean_scores,test_mean_scores = Linear_svc_mean_Score(X_pca,cancer.target,num)
#print("The train scores of MinMaxScaler transformed(PCA(2)) data :",train_mean_scores)
print("The test scores of MinMaxScaler transformed(PCA(2)) data :",test_mean_scores)

#在RobustScaler基础上，选择两个主成分
R_scaler = RobustScaler()
R_scaler.fit(cancer.data)
cancer_R_Scaler = R_scaler.transform(cancer.data)
train_mean_scores,test_mean_scores = Linear_svc_mean_Score(cancer_R_Scaler,cancer.target,num)
#print("The train scores of RobustScaler transformed data :",train_mean_scores)
print("The test scores of RobustScaler transformed data :",test_mean_scores)

#在RobustScaler基础上，选择两个主成分
pca = PCA(n_components = 3)
pca.fit(cancer_R_Scaler)
X_pca = pca.transform(cancer_R_Scaler)
X_train,X_test,y_train,y_test = train_test_split(X_pca,cancer.target,stratify=cancer.target,random_state=60)
#查看PCA降维后的数据类型
print("PCA(2) data : " ,X_train.shape,X_train[0])
train_mean_scores,test_mean_scores = Linear_svc_mean_Score(X_pca,cancer.target,num)
#print("The train scores of RobustScaler transformed(PCA(2)) data :",train_mean_scores)
print("The test scores of RobustScaler transformed(PCA(2)) data :",test_mean_scores)

参考书籍：《python机器学习基础教程》